Моделирование - одна из центральных тем информатики. Потенциал Desmos как эффективного инструмента для создания и исследования различных моделей очень большой. Примеры моделей, которые представлены ниже, можно создать и другими средствами, например, с помощью программ, написанных на Лого или Паскале. Но здесь важно, во-первых, что ученики знакомятся с новыми подходами в разработке и исследовании компьютерных моделей. Во вторых, Desmos - современный облачный инструмент. А это означает, что вокруг него сформировалось сообщество заинтересованных людей - профессионалов и любителей, которые щедро делятся своими идеями и помогают новичкам. В постоянно пополняющейся коллекции Desmos-проектов заинтересованный ученик может найти решение своих вопросов и почерпнуть вдохновение для собственных проектов.
Что же привлекает в Desmos и делает его ценным образовательным инструментом для моделирования и исследования моделей?
1. Desmos прекрасно справляется с графиками функций, заданных параметрически. Это дает возможность построить и исследовать, например, такие кривые как "классическая" циклоида или удлиненная/укороченная циклоида, траектория карандаша в спирографе.
Образовательная ценность такой деятельности?
Во-первых, освоение и использование современного программного обеспечения для решения практических задач.
Во-вторых, знакомство на практике с параметрическими кривыми и визуализация процесса их построения, где параметр в полученной динамической модели можно интерпретировать как время. Использование подвижных точек делает картину предельно наглядной. Опыт соединения "математических абстракций" с движением реальных объектов также заслуживает внимания.
В-третьих, красивая динамическая графика может быть прекрасным дополнением к сообщениям об этих интересных кривых, сделанных перед одноклассниками, с историческими фактами и фактами из области физики.
2. Все сказанное относится и к полярным координатам, с помощью которых можно решить задачу о траектории муравья, который ползет по вращающейся веточке.
Спираль Архимеда

3. Подвижные точки, возможность построения графиков функций, заданных различными способами, позволят ученику самостоятельно или под руководством учителя не только исследовать, но и построить интересные динамические модели, примеры которых приведены ниже.
Продолжение следует
Что же привлекает в Desmos и делает его ценным образовательным инструментом для моделирования и исследования моделей?
1. Desmos прекрасно справляется с графиками функций, заданных параметрически. Это дает возможность построить и исследовать, например, такие кривые как "классическая" циклоида или удлиненная/укороченная циклоида, траектория карандаша в спирографе.
Образовательная ценность такой деятельности?
Во-первых, освоение и использование современного программного обеспечения для решения практических задач.
Во-вторых, знакомство на практике с параметрическими кривыми и визуализация процесса их построения, где параметр в полученной динамической модели можно интерпретировать как время. Использование подвижных точек делает картину предельно наглядной. Опыт соединения "математических абстракций" с движением реальных объектов также заслуживает внимания.
В-третьих, красивая динамическая графика может быть прекрасным дополнением к сообщениям об этих интересных кривых, сделанных перед одноклассниками, с историческими фактами и фактами из области физики.
| Спирограф | Циклоида | Укороченная (удлиненная) циклоида |
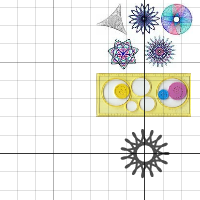 |
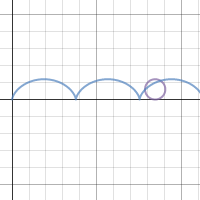 |
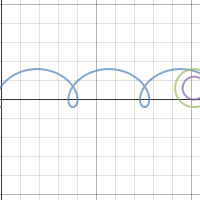 |
2. Все сказанное относится и к полярным координатам, с помощью которых можно решить задачу о траектории муравья, который ползет по вращающейся веточке.
Спираль Архимеда

3. Подвижные точки, возможность построения графиков функций, заданных различными способами, позволят ученику самостоятельно или под руководством учителя не только исследовать, но и построить интересные динамические модели, примеры которых приведены ниже.
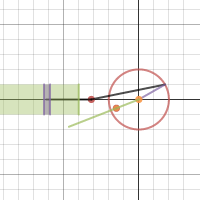
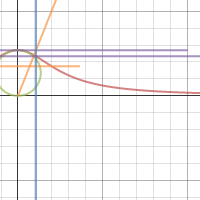
| Геометрическая иллюстрация к параметрическому заданию эллипса | Превращение вращательного движения в поступательное | "Локон Аньези" |
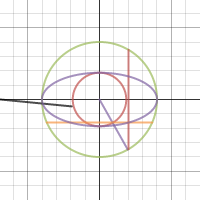 |
 |
 |
Продолжение следует
1 комментарий:
"Локон Аньези" , мое любимое, Ольга! Курсовая работа по ней:)
Отправить комментарий